I originally submitted this under Technical Articles - but that went nowhere.
GETTING (A LOT) MORE POWER FROM SQUIRREL CAGE MOTORS
If your lathe or milling machine has a 3 phase motor and you have often wished it had more power.
Or you are thinking of changing to an inverter drive or you need to rewind your motor.
Well now is the time to consider getting more power while you are at it.
FIRST CAUTION: Most machine tools (particularly the “good” ones) will have the various drive components sized to match the available horsepower and will not necessarily handle more. You be the judge and on your head be it.
If you are changing to an inverter drive in order to use its variable speed features then upping your power will be advantageous at the lower end.
SECOND CAUTION: The extra power comes from extra speed – you will need to change or adapt your primary drive ratio.
The following article uses European 380V / 50 Hz as a starting point – you just have to use the same rules to adapt to 60Hz etc.
SQUIRREL CAGE MOTORS
The power output of a conventional squirrel cage motor is limited by two factors :-
1) Its Torque output which is determined by the magnetic saturation of the iron core / rotor components.
2) Its speed (rpm) which is determined by frequency and number of poles.
The torque is limited by the magnetic saturation of the rotor & stator and is determined by the laws of physics – so the more torque you need, the more iron has to be designed into the motor – pretty much regardless of the motor type.
It is the speed limit imposed by frequency – maximum 3000 rpm @ 50 Hz. (for a 2 Pole motor) – which curtails the power that might otherwise be available.
Conventional squirrel cage motors are therefore relatively bulky and heavy for their output – this is why they are never used in hand held power tools – instead brush motors are used – since these can typically spin at 20000-30000 rpm then for the same torque ( think mass ) 10 times the power can be delivered.
You can of course speed up a 3 phase squirrel cage motor by using an inverter to run it at a higher frequency – but you will run into a power limiting problem viz :-
If you take a 380V 3 phase motor and run it off an inverter – the inverter will ramp up the voltage with frequency viz :-
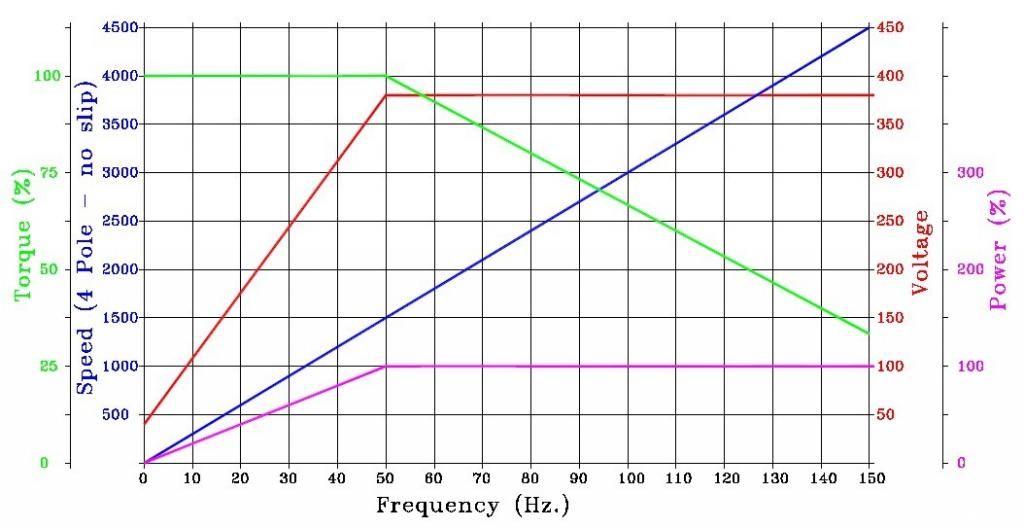
The voltage ramps up according to a V=mF+c function – in this case c (constant or starting voltage) is 40 volts at Zero Hz. Ramping up to 380 Volts at 50 Hz.
(V being the voltage, m being the multiplier and F the frequency).
(The graphics assume no slip i.e. synchronous speed is achieved – slip is normally about 5% - the assumed linearity is for simplicity / illustrative purpose)
One advantage of using an inverter is that you can get (near) constant torque out of a squirrel cage motor (normally starting torque is terrible if started direct on line – this is because at switch on the rotor is standing still and its impedance is at 50Hz.
If the motor’s rated torque is at 5% slip – ie 2.5Hz (as “seen” by the squirrel cage bars) then its starting torque is only 5% of its rated torque – or rated torque x slip). The ramp up function of an inverter allows you to keep the disparity between the rotor and field rpm to a minimum during starting – particularly with high inertia loads.
Torque is directly proportional to current (other than in stall or outside of saturation = abnormal conditions) which in turn is dependant on Voltage/Impedance which is dependant on frequency (ignoring the small resistive component) hence the reason for ramping up the voltage with the frequency.
The problem comes in at the top end where the inverter flat lines at 380V (Only 220V if you are using a single phase to 3 phase inverter).
So from this point onward any increase in speed (frequency) results in an increase in impedance and concomitant loss of torque.
So from this point onward the power output “flatlines” (Revs go up, torque goes down and resultant power is constant)
In order to get more power from our motor we need to keep pushing the voltage higher to overcome the frequency imparted impedance in order to keep up the torque.
Since the inverter voltage won’t go any higher the only option we have going for us is to rewind the motor to a lower 50 Hz. Rated Voltage.
The following graphic shows the same motor but rewound for 157 Volts @ 50 Hz.
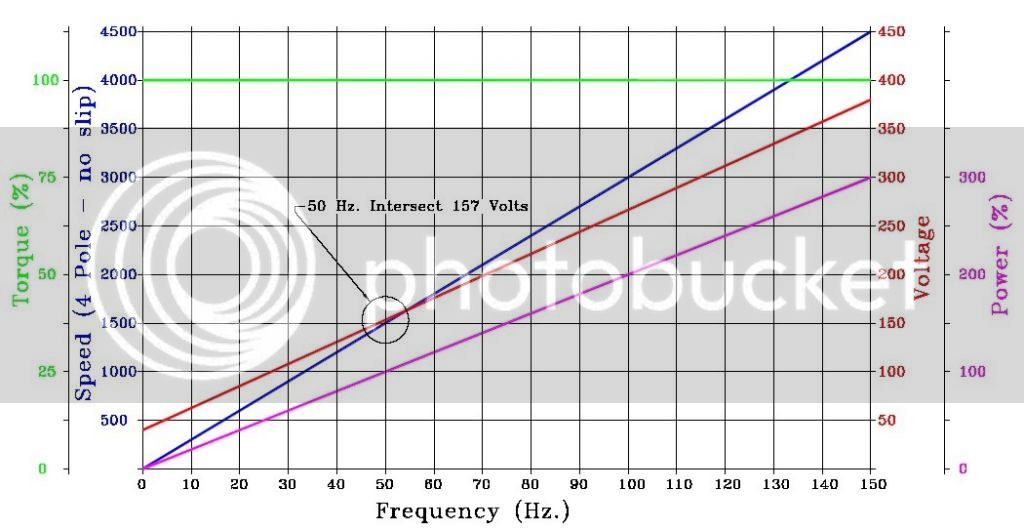
Now the inverter ramps up so that at 50 Hz we are indeed at the rated 157 Volts – only now we can keep pushing the voltage with frequency up to 380v at 150 Hz. thereby maintaining the torque.
So now we can run the motor 3 times faster (as illustrated) and get 3 times more power from the same frame size.
We might of course have to gear down this speed to get the power at the desired output speed (as with hand power tools).
So How Far Can We Push This ?
Pretty much as far as you like within the speed rating of the ball bearings (which can be changed to closer fit spec. / higher speed ratings) or a far as you can spin the motor without risking it coming apart.
For motors up to about 3kW you can safely go to 12000 rpm which on a 4 pole motor would be 8 times its rated speed and hence power output. Smaller motors can be pushed to 24000 rpm but you need to consider the failure speed of the rotor or fan as well as using selected fit bearings and fine balancing.
(Note: A Ø30mm shaft deep groove ball bearing has an 11000-20000 rpm speed rating and much higher as you go smaller – 24000-38000 for a Ø15mm shaft .)
It’s a pretty neat trick getting 24kW out of a 3kW motor.
Remember the only thing you are doing is spinning it faster – its rated torque remains unchanged therefore the overall ampere●turns / field saturation remains unchanged.
Heat Problems
The copper losses (I²R) losses will be approximately the same – since the rewind uses heavier wire – its cross sectional area changes per the ratio change– but the length of the wire is reduced by the same ratio – so the I²R is unchanged as a result of the cross sectional wire area change. (Greatly dependant on the actual wire gauge chosen by the rewinder.)
Explanation : If we halve the turns and double the current then the I² component is 4 times bigger but the cross sectional area of the wire is doubled halving its resistance, but its length is also halved so the resistance is ¼ of what it was, so overall our I²R remains unchanged. (2xI)²R/4 = I²R
The Iron losses (Hysterysis & Eddy Current losses) will increase with the increased frequency due to an increase in Hysteresis losses while Eddy Current losses remain approximately the same (as there is no change in the ampere●turns / field saturation although here we might push a further 10% or so – see later).
Mechanical losses to cooling airflow and friction in the bearings will also increase but is not significant.
However the cooling airflow from the fan turning at much higher speed offers significantly greater cooling than additional heat created.
Overall the motor generates more heat but the increased cooling is generally more than sufficient to offset this.
Typically losses in a motor are 50% to copper losses, 20% to Hysteresis losses, 25% to Eddy Current Losses & 5% to mechanical losses.
So for a doubling of speed we get approximately 25% more heat – but approximately double the cooling airflow – hence the comment that the increased airflow is generally sufficient to take care of the increased heat. (These figures vary considerably ±10% from motor to motor but the increase in fan speed will easily offset any increase in heat – unless you run beyond saturation and into overcurrent – which will destroy any motor.)
What should also be apparent is that running a motor at higher speed actually improves its efficiency.
A word of caution – you can run into a problem where the extra iron loss heat cannot conduct out to the cooling fins fast enough – in which case you will need to de-rate the motor slightly. To check for this monitor the temperature of the case under load until it stabilises – firstly is this temperature within the range of “normal” – 40°C to 60°C over ambient (what was the donor motor’s originals rating) – secondly on stopping the motor does this temperature continue to rise significantly – indicating that the core is running considerably hotter than the external temperature suggests.
Using a quality brand high duty cycle (S1 = 100% duty rating) donor motor in the first place will obviously help. (S2 = Intermittent duty & S3 = Light duty cycle.)
Increased Iron losses in the rotor will also increase the rotor temperature and rotor shaft / bearing temperature which is detrimental to bearing life. Again the selection of a quality brand which has cooling blades cast into the aluminium end rings of the rotor will perform better than plain end rings.
Note: – problems do set in when motors are run “slowly” off inverters – forced cooling by external constant speed fans is then required – the rule here is not to run an “overclocked” motor too slowly (or add external fans).
Since the donor motor was never intended to run at a higher speed, additional fine balancing might also be required particularly if vibration is going to be an issue.
All in all it generally presents no problem but err on the side of caution as the duty cycle increases and be very wary of running overclocked motors at 100% of their now overrated output 100% of the time – although this is possible (it depends).
If these sort of speeds bother you, then consider your typical wire wound armatures of power tools (of similar diameters) that spin at typical speeds of 20000 to 30000 rpm – these open frame windings are considerably more fragile than a stocky, closed lamination squirrel cage with its cast in-situ aluminium conductor bars. Typically the plastic fan is likely to fly apart long before the rotor.
Why Would You Want To Do This ?
Any application where power to weight ratios are a problem (such as in power tools for robotic applications) or where you have space or weight constraints and need more power out of a smaller frame.
Typically also where you have a space constrained existing motor that you need to get more out of.
High frequency motors specifically built for high spindle rpm are available but are generally very expensive (usually built to grinding spindle accuracy – which might be overkill in many applications). These motors also tend to use long rotors to improve torque to keep the diameter of the motor down (at the expense of length).
FYI – Commercial airliners use 400 Hz specifically to reduce the mass of electric motors used throughout their control systems (more power per unit weight).
How Do You Do This ?
Firstly determine what power you want, what speed and what frame size motor you wish to use (or whatever it is your are stuck with starting with).
If you require a low final drive speed, consider how you are going to gear it down taking care not to exceed pitch circle velocity limits of gear and toothed drive belts etc. – for this reason you might like to start with a 4 pole (1500 rpm) or 6 pole (1000 rpm) motor to reduce the effort in gearing down later.
So lets say we have in mind a 3kW x 380V 4 Pole motor with a rated output of 1425rpm (as a result of “slip” the rotor must turn somewhat slower than the field in order for current to be generated in the squirrel cage bars and is typically - as in this case - 5%)
We require 15kW – so we have to spin this motor 15/3 = 5 times faster – so we are going to run it at 5 x 50 = 250 Hz.
To determine the 50Hz rewind voltage we firstly need to know the V=mF+c function of the unmodified donor motor. (Note: This linear function is a generally accepted practice approximation of a slightly non-linear function – for simplicity.)
One “guestimate” is to presume c is a function of the “slip” so we take its rated speed versus its synchronous speed 1425/1500 = 95% or 5% slip.
Then c = 380 x 0.05 = 19 Volts.
A more complicated and correct way is to run the motor {no load} off the inverter at a variety of lower speeds and push the voltage up at each point until we start seeing a disproportionate increase in current with voltage which means we have exceeded saturation – do this for several data points and you will get a graph something like the following :-
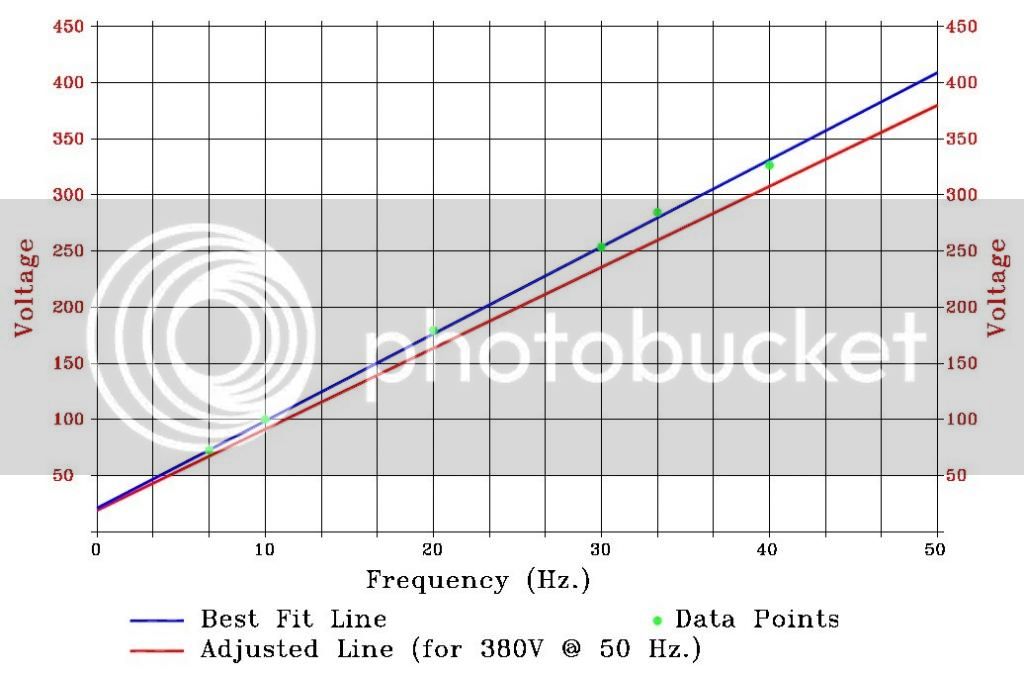
[ Note: Some inverters (Yaskawa) have an “Autotune” function and the inverter determines & sets these values (in much the same way – by pushing the voltage until current / voltage disparity indicates saturation) – the determined values can then be looked up from the display. ]
Our best fit line projects a 50Hz saturation limit of 418 Volts (which is about what you would expect since the manufacturers typically allow for 10% over voltage conditions) and a Zero Hz. Voltage of 21 Volts.
Adjusting this back (in this case by 90% - from the above saturation vs specification) we get the unmodified donor motor specification line from 19 Volts to 380 Volts.
Note: When running off an inverter, its output voltage is unaffected by input voltage fluctuations (within reason) and you can run the motor much closer to saturation than you would dare with direct on line – so typically there is another 10% or so power to be gained here as well by not adjusting back from saturation vs specification (let the autotune take care of it).
So now we know our V=mF+c function of the motor. (We might also try asking the motor manufacturer – but that can open a whole can of worms – alternately choose a figure between 5 & 10% for c as a rule of thumb.
A further rule of thumb to determine the 50Hz wind value is simply divide the voltage by the amount you are going to goose it up – in this case 380/5 = 76V and then add the slippage (5%) = 79.8V which is pretty close to the more complicated calculations.)
Our V=mF+c function gives 19 + 7.22F so for a frequency of 40 Hz we would set the inverter to 19 + 7.22 x 40 = 307.8 Volts etc.
Now we have to imagine we are going to run at 250 Hz. (re prior determination) and we would require 19 + 7.22 x 250 = 1824 Volts
Let x = revised winding ratio
Then 19 x +7.22 x x 250 = 380 (both constant & multiplier are involved)
Therefore 1824 x = 380
Therefore x = 380/1824 = 0.208333
So we rewind the motor for 380 x 0.208333 = 79.2 volts
The armature rewinder must replace the existing windings with 20.8% the number of turns of the original windings – using commensurately thicker wire. ie if it was 100 turns then it must now be 21 - if the wire was Ø0.55mm it will need to increase to 0.55 x ²√(100/21) = 0.55x2.182 = Ø1.2
Rather than explaining yourself its often easier to simply tell the rewinder “Here, rewind this 380V motor to suit 80V” that way you avoid getting involved in a long technical debate as to why you can’t do what you’re trying to do.
(The standard response from most motor manufactures and rewinders is “You can’t do that ! ” – they are wrong ! – if you find a technically savvy engineer they will understand – salesmen – forget it – dumb as a box of rocks.)
Your rewound motor now has the V=mF+c function (multiply by your x value) of
3.96 + 1.5041F
for 50Hz = 79.2 Volts (our rewind specification for 50 Hz.)
for 250Hz = 380 Volts (Our target top end.) Which is what we were looking for.
Remember (from the above) your current is now going to be 5 times higher (the power has to come from somewhere). So the inverter has to be large enough (15kW in above example) to drive it. (You might be able to get 15 kW out of a 3 kW motor but you can’t get 15 kW out of a 3 kW inverter.)
After rewinding we can again use the “Autotune” feature to set up the rewound motor.
Note: Depending on configuration the “Autotune” feature may set up the correct non-linear relationship as a series of 3 or 4 straight line relationships to further optimise the set- up.
As a final precaution – re-mark the rating plate – just in case some idiot tries to connect it to 380V @ 50 Hz. – in which case all the blue smoke packed into the motor by the rewinder will come pouring out. (This motor’s rating is now 380V @ 250Hz – so just add a 2 before the 50 on the rating plate so it now reads 250Hz.)
Below a “tiny” 300W 240V single phase, rewound to 112V three phase (@ 50 Hz.) run at 380V @ 200 Hz (12000 rpm) producing 1.2 kW.

The coin (Ø26mm) for size comparison. This is a very small motor for 1.2kW - QED
Cost of rewind is no big deal !
Finally – motor manufacturers are now required to classify the efficiency of their machines according to specifications still being formulated / evolving :-
Class 1 = High Efficiency
Class 2 = Medium Efficiency
Class 3 = Low Efficiency
Since efficiency is mostly a function of heat lost to iron and copper losses it is obvious that you should start with a high efficiency motor as a donor for your project.
i.e. Start with an S1 Eff. 1 frame motor from a quality manufacturer and you can’t go wrong !
A “Quick & Dirty” 70% More Power.
Most smaller three phase motors have six terminals which can be bridged to “Star” connection for 380V or “Delta” for 220V – so here we can simply wire up in “Delta” but run it at 380V at an appropriately higher frequency.
Using our previous example of a 3kW motor with c=19V @ 0Hz and 380 @ 50Hz in “star” would be c=11V @ 0Hz and 220 @ 50Hz so :-
m = (220-11)/50 = 4.18 V/Hz.
So to run this configuration up to 380V :-
(380-11)/4.18 = 88.3 Hz or ±2516 rpm (4 pole, 5% slip) vs prior 1425 rpm or 76% more power.
Remember, you will only derive an improvement in torque if you gear down by the same ratio.
For this “trick” to work, your inverter output voltage must exceed the motors normal voltage.
Final Caution: Raising the voltage on a three phase motor will not make it turn any faster (as is the case for a D.C. motor). You can only raise its speed by raising the driving frequency – but this raises the impedance and for that you do need to raise the voltage if you want to maintain the current & torque.
Have Fun,
Ken
GETTING (A LOT) MORE POWER FROM SQUIRREL CAGE MOTORS
If your lathe or milling machine has a 3 phase motor and you have often wished it had more power.
Or you are thinking of changing to an inverter drive or you need to rewind your motor.
Well now is the time to consider getting more power while you are at it.
FIRST CAUTION: Most machine tools (particularly the “good” ones) will have the various drive components sized to match the available horsepower and will not necessarily handle more. You be the judge and on your head be it.
If you are changing to an inverter drive in order to use its variable speed features then upping your power will be advantageous at the lower end.
SECOND CAUTION: The extra power comes from extra speed – you will need to change or adapt your primary drive ratio.
The following article uses European 380V / 50 Hz as a starting point – you just have to use the same rules to adapt to 60Hz etc.
SQUIRREL CAGE MOTORS
The power output of a conventional squirrel cage motor is limited by two factors :-
1) Its Torque output which is determined by the magnetic saturation of the iron core / rotor components.
2) Its speed (rpm) which is determined by frequency and number of poles.
The torque is limited by the magnetic saturation of the rotor & stator and is determined by the laws of physics – so the more torque you need, the more iron has to be designed into the motor – pretty much regardless of the motor type.
It is the speed limit imposed by frequency – maximum 3000 rpm @ 50 Hz. (for a 2 Pole motor) – which curtails the power that might otherwise be available.
Conventional squirrel cage motors are therefore relatively bulky and heavy for their output – this is why they are never used in hand held power tools – instead brush motors are used – since these can typically spin at 20000-30000 rpm then for the same torque ( think mass ) 10 times the power can be delivered.
You can of course speed up a 3 phase squirrel cage motor by using an inverter to run it at a higher frequency – but you will run into a power limiting problem viz :-
If you take a 380V 3 phase motor and run it off an inverter – the inverter will ramp up the voltage with frequency viz :-

The voltage ramps up according to a V=mF+c function – in this case c (constant or starting voltage) is 40 volts at Zero Hz. Ramping up to 380 Volts at 50 Hz.
(V being the voltage, m being the multiplier and F the frequency).
(The graphics assume no slip i.e. synchronous speed is achieved – slip is normally about 5% - the assumed linearity is for simplicity / illustrative purpose)
One advantage of using an inverter is that you can get (near) constant torque out of a squirrel cage motor (normally starting torque is terrible if started direct on line – this is because at switch on the rotor is standing still and its impedance is at 50Hz.
If the motor’s rated torque is at 5% slip – ie 2.5Hz (as “seen” by the squirrel cage bars) then its starting torque is only 5% of its rated torque – or rated torque x slip). The ramp up function of an inverter allows you to keep the disparity between the rotor and field rpm to a minimum during starting – particularly with high inertia loads.
Torque is directly proportional to current (other than in stall or outside of saturation = abnormal conditions) which in turn is dependant on Voltage/Impedance which is dependant on frequency (ignoring the small resistive component) hence the reason for ramping up the voltage with the frequency.
The problem comes in at the top end where the inverter flat lines at 380V (Only 220V if you are using a single phase to 3 phase inverter).
So from this point onward any increase in speed (frequency) results in an increase in impedance and concomitant loss of torque.
So from this point onward the power output “flatlines” (Revs go up, torque goes down and resultant power is constant)
In order to get more power from our motor we need to keep pushing the voltage higher to overcome the frequency imparted impedance in order to keep up the torque.
Since the inverter voltage won’t go any higher the only option we have going for us is to rewind the motor to a lower 50 Hz. Rated Voltage.
The following graphic shows the same motor but rewound for 157 Volts @ 50 Hz.

Now the inverter ramps up so that at 50 Hz we are indeed at the rated 157 Volts – only now we can keep pushing the voltage with frequency up to 380v at 150 Hz. thereby maintaining the torque.
So now we can run the motor 3 times faster (as illustrated) and get 3 times more power from the same frame size.
We might of course have to gear down this speed to get the power at the desired output speed (as with hand power tools).
So How Far Can We Push This ?
Pretty much as far as you like within the speed rating of the ball bearings (which can be changed to closer fit spec. / higher speed ratings) or a far as you can spin the motor without risking it coming apart.
For motors up to about 3kW you can safely go to 12000 rpm which on a 4 pole motor would be 8 times its rated speed and hence power output. Smaller motors can be pushed to 24000 rpm but you need to consider the failure speed of the rotor or fan as well as using selected fit bearings and fine balancing.
(Note: A Ø30mm shaft deep groove ball bearing has an 11000-20000 rpm speed rating and much higher as you go smaller – 24000-38000 for a Ø15mm shaft .)
It’s a pretty neat trick getting 24kW out of a 3kW motor.
Remember the only thing you are doing is spinning it faster – its rated torque remains unchanged therefore the overall ampere●turns / field saturation remains unchanged.
Heat Problems
The copper losses (I²R) losses will be approximately the same – since the rewind uses heavier wire – its cross sectional area changes per the ratio change– but the length of the wire is reduced by the same ratio – so the I²R is unchanged as a result of the cross sectional wire area change. (Greatly dependant on the actual wire gauge chosen by the rewinder.)
Explanation : If we halve the turns and double the current then the I² component is 4 times bigger but the cross sectional area of the wire is doubled halving its resistance, but its length is also halved so the resistance is ¼ of what it was, so overall our I²R remains unchanged. (2xI)²R/4 = I²R
The Iron losses (Hysterysis & Eddy Current losses) will increase with the increased frequency due to an increase in Hysteresis losses while Eddy Current losses remain approximately the same (as there is no change in the ampere●turns / field saturation although here we might push a further 10% or so – see later).
Mechanical losses to cooling airflow and friction in the bearings will also increase but is not significant.
However the cooling airflow from the fan turning at much higher speed offers significantly greater cooling than additional heat created.
Overall the motor generates more heat but the increased cooling is generally more than sufficient to offset this.
Typically losses in a motor are 50% to copper losses, 20% to Hysteresis losses, 25% to Eddy Current Losses & 5% to mechanical losses.
So for a doubling of speed we get approximately 25% more heat – but approximately double the cooling airflow – hence the comment that the increased airflow is generally sufficient to take care of the increased heat. (These figures vary considerably ±10% from motor to motor but the increase in fan speed will easily offset any increase in heat – unless you run beyond saturation and into overcurrent – which will destroy any motor.)
What should also be apparent is that running a motor at higher speed actually improves its efficiency.
A word of caution – you can run into a problem where the extra iron loss heat cannot conduct out to the cooling fins fast enough – in which case you will need to de-rate the motor slightly. To check for this monitor the temperature of the case under load until it stabilises – firstly is this temperature within the range of “normal” – 40°C to 60°C over ambient (what was the donor motor’s originals rating) – secondly on stopping the motor does this temperature continue to rise significantly – indicating that the core is running considerably hotter than the external temperature suggests.
Using a quality brand high duty cycle (S1 = 100% duty rating) donor motor in the first place will obviously help. (S2 = Intermittent duty & S3 = Light duty cycle.)
Increased Iron losses in the rotor will also increase the rotor temperature and rotor shaft / bearing temperature which is detrimental to bearing life. Again the selection of a quality brand which has cooling blades cast into the aluminium end rings of the rotor will perform better than plain end rings.
Note: – problems do set in when motors are run “slowly” off inverters – forced cooling by external constant speed fans is then required – the rule here is not to run an “overclocked” motor too slowly (or add external fans).
Since the donor motor was never intended to run at a higher speed, additional fine balancing might also be required particularly if vibration is going to be an issue.
All in all it generally presents no problem but err on the side of caution as the duty cycle increases and be very wary of running overclocked motors at 100% of their now overrated output 100% of the time – although this is possible (it depends).
If these sort of speeds bother you, then consider your typical wire wound armatures of power tools (of similar diameters) that spin at typical speeds of 20000 to 30000 rpm – these open frame windings are considerably more fragile than a stocky, closed lamination squirrel cage with its cast in-situ aluminium conductor bars. Typically the plastic fan is likely to fly apart long before the rotor.
Why Would You Want To Do This ?
Any application where power to weight ratios are a problem (such as in power tools for robotic applications) or where you have space or weight constraints and need more power out of a smaller frame.
Typically also where you have a space constrained existing motor that you need to get more out of.
High frequency motors specifically built for high spindle rpm are available but are generally very expensive (usually built to grinding spindle accuracy – which might be overkill in many applications). These motors also tend to use long rotors to improve torque to keep the diameter of the motor down (at the expense of length).
FYI – Commercial airliners use 400 Hz specifically to reduce the mass of electric motors used throughout their control systems (more power per unit weight).
How Do You Do This ?
Firstly determine what power you want, what speed and what frame size motor you wish to use (or whatever it is your are stuck with starting with).
If you require a low final drive speed, consider how you are going to gear it down taking care not to exceed pitch circle velocity limits of gear and toothed drive belts etc. – for this reason you might like to start with a 4 pole (1500 rpm) or 6 pole (1000 rpm) motor to reduce the effort in gearing down later.
So lets say we have in mind a 3kW x 380V 4 Pole motor with a rated output of 1425rpm (as a result of “slip” the rotor must turn somewhat slower than the field in order for current to be generated in the squirrel cage bars and is typically - as in this case - 5%)
We require 15kW – so we have to spin this motor 15/3 = 5 times faster – so we are going to run it at 5 x 50 = 250 Hz.
To determine the 50Hz rewind voltage we firstly need to know the V=mF+c function of the unmodified donor motor. (Note: This linear function is a generally accepted practice approximation of a slightly non-linear function – for simplicity.)
One “guestimate” is to presume c is a function of the “slip” so we take its rated speed versus its synchronous speed 1425/1500 = 95% or 5% slip.
Then c = 380 x 0.05 = 19 Volts.
A more complicated and correct way is to run the motor {no load} off the inverter at a variety of lower speeds and push the voltage up at each point until we start seeing a disproportionate increase in current with voltage which means we have exceeded saturation – do this for several data points and you will get a graph something like the following :-

[ Note: Some inverters (Yaskawa) have an “Autotune” function and the inverter determines & sets these values (in much the same way – by pushing the voltage until current / voltage disparity indicates saturation) – the determined values can then be looked up from the display. ]
Our best fit line projects a 50Hz saturation limit of 418 Volts (which is about what you would expect since the manufacturers typically allow for 10% over voltage conditions) and a Zero Hz. Voltage of 21 Volts.
Adjusting this back (in this case by 90% - from the above saturation vs specification) we get the unmodified donor motor specification line from 19 Volts to 380 Volts.
Note: When running off an inverter, its output voltage is unaffected by input voltage fluctuations (within reason) and you can run the motor much closer to saturation than you would dare with direct on line – so typically there is another 10% or so power to be gained here as well by not adjusting back from saturation vs specification (let the autotune take care of it).
So now we know our V=mF+c function of the motor. (We might also try asking the motor manufacturer – but that can open a whole can of worms – alternately choose a figure between 5 & 10% for c as a rule of thumb.
A further rule of thumb to determine the 50Hz wind value is simply divide the voltage by the amount you are going to goose it up – in this case 380/5 = 76V and then add the slippage (5%) = 79.8V which is pretty close to the more complicated calculations.)
Our V=mF+c function gives 19 + 7.22F so for a frequency of 40 Hz we would set the inverter to 19 + 7.22 x 40 = 307.8 Volts etc.
Now we have to imagine we are going to run at 250 Hz. (re prior determination) and we would require 19 + 7.22 x 250 = 1824 Volts
Let x = revised winding ratio
Then 19 x +7.22 x x 250 = 380 (both constant & multiplier are involved)
Therefore 1824 x = 380
Therefore x = 380/1824 = 0.208333
So we rewind the motor for 380 x 0.208333 = 79.2 volts
The armature rewinder must replace the existing windings with 20.8% the number of turns of the original windings – using commensurately thicker wire. ie if it was 100 turns then it must now be 21 - if the wire was Ø0.55mm it will need to increase to 0.55 x ²√(100/21) = 0.55x2.182 = Ø1.2
Rather than explaining yourself its often easier to simply tell the rewinder “Here, rewind this 380V motor to suit 80V” that way you avoid getting involved in a long technical debate as to why you can’t do what you’re trying to do.
(The standard response from most motor manufactures and rewinders is “You can’t do that ! ” – they are wrong ! – if you find a technically savvy engineer they will understand – salesmen – forget it – dumb as a box of rocks.)
Your rewound motor now has the V=mF+c function (multiply by your x value) of
3.96 + 1.5041F
for 50Hz = 79.2 Volts (our rewind specification for 50 Hz.)
for 250Hz = 380 Volts (Our target top end.) Which is what we were looking for.
Remember (from the above) your current is now going to be 5 times higher (the power has to come from somewhere). So the inverter has to be large enough (15kW in above example) to drive it. (You might be able to get 15 kW out of a 3 kW motor but you can’t get 15 kW out of a 3 kW inverter.)
After rewinding we can again use the “Autotune” feature to set up the rewound motor.
Note: Depending on configuration the “Autotune” feature may set up the correct non-linear relationship as a series of 3 or 4 straight line relationships to further optimise the set- up.
As a final precaution – re-mark the rating plate – just in case some idiot tries to connect it to 380V @ 50 Hz. – in which case all the blue smoke packed into the motor by the rewinder will come pouring out. (This motor’s rating is now 380V @ 250Hz – so just add a 2 before the 50 on the rating plate so it now reads 250Hz.)
Below a “tiny” 300W 240V single phase, rewound to 112V three phase (@ 50 Hz.) run at 380V @ 200 Hz (12000 rpm) producing 1.2 kW.

The coin (Ø26mm) for size comparison. This is a very small motor for 1.2kW - QED
Cost of rewind is no big deal !
Finally – motor manufacturers are now required to classify the efficiency of their machines according to specifications still being formulated / evolving :-
Class 1 = High Efficiency
Class 2 = Medium Efficiency
Class 3 = Low Efficiency
Since efficiency is mostly a function of heat lost to iron and copper losses it is obvious that you should start with a high efficiency motor as a donor for your project.
i.e. Start with an S1 Eff. 1 frame motor from a quality manufacturer and you can’t go wrong !
A “Quick & Dirty” 70% More Power.
Most smaller three phase motors have six terminals which can be bridged to “Star” connection for 380V or “Delta” for 220V – so here we can simply wire up in “Delta” but run it at 380V at an appropriately higher frequency.
Using our previous example of a 3kW motor with c=19V @ 0Hz and 380 @ 50Hz in “star” would be c=11V @ 0Hz and 220 @ 50Hz so :-
m = (220-11)/50 = 4.18 V/Hz.
So to run this configuration up to 380V :-
(380-11)/4.18 = 88.3 Hz or ±2516 rpm (4 pole, 5% slip) vs prior 1425 rpm or 76% more power.
Remember, you will only derive an improvement in torque if you gear down by the same ratio.
For this “trick” to work, your inverter output voltage must exceed the motors normal voltage.
Final Caution: Raising the voltage on a three phase motor will not make it turn any faster (as is the case for a D.C. motor). You can only raise its speed by raising the driving frequency – but this raises the impedance and for that you do need to raise the voltage if you want to maintain the current & torque.
Have Fun,
Ken